18 Neighborhood analysis

18.1 Preamble

18.1.1 Introduction

Neighborhood analysis aims to investigate the composition of and interaction between cells and cell types within small regions of tissue, which are referred to as neighborhoods or niches.

18.1.2 Dependencies

Code

library(dplyr)
library(tidyr)
library(ggplot2)
library(patchwork)
library(RColorBrewer)
library(BiocParallel)
library(SpatialExperiment)

Code

# load data from previous section
spe <- readRDS("img-spe_cl.rds")
spe$k <- colLabels(spe)

Code

# basic theme for spatial plots
theme_xy <- list(
    coord_equal(expand=FALSE), 
    theme_void(), theme(
        plot.margin=margin(l=5),
        legend.key=element_blank(),
        panel.background=element_rect(fill="black")))

18.2 Nearest neighbors

Custom spatial analyses may rely on identifying nearest neighbors (NNs) of cells. We recommend RANN for this purpose, which finds NNs in \(O(N\log N)\) time for \(N\) cells (c.f., conventional approaches would take \(O(N^2)\) time) by relying on a Approximate Near Neighbor (ANN) C++ library. Furthermore, there is support for exact, approximate, and fixed-radius searchers. The latter is of particular interest in biology; e.g., one might require \(k\)NNs to lie within a biologically sensible distance as to avoid consideration of cells that are far-off, especially in sparse regions or at tissue borders.

As a toy example, we here compute the \(k\)NNs between a pair of subpopulations, with and without thresholding on NN distances (searchtype="radius").

For the first approach, each cell will receive \(k\) neighbors exactly,
but these may lie within an arbitrary distance.
For the second approach, cells will receive \(\leq k\) neighbors,
depending on how many cells lie within a radius \(r\).

Code

library(RANN)
k <- 10 # num. neighbors
r <- 50 # dist. threshold
i <- spe$k == 1 # source
j <- spe$k == 4 # target
xy <- spatialCoords(spe)
# k-NN search: all cells have k neighbors
ns_k <- nn2(xy[j, ], xy[i, ], k=k)
is_k <- ns_k$nn.idx
all(rowSums(is_k > 0) == k) 
# w/ fixed-radius: cells have 0-k neighbors
ns_r <- nn2(xy[j, ], xy[i, ], k=k, searchtype="radius", r=r)
is_r <- ns_r$nn.idx
range(rowSums(is_r > 0))

##  [1] TRUE
##  [1]  0 10

The neighbors obtained via fixed-radius search (right) are less scattered than those obtained for unlimited distances (left); the former are arguably more meaningful in a biological context:

Code

df <- data.frame(xy, colData(spe))
p0 <- ggplot(df, aes(x_centroid, y_centroid)) + 
    geom_point(data=df, col="navy", shape=16, size=0) +
    geom_point(data=df[i, ], col="magenta", shape=16, size=0) 
p1 <- p0 + geom_point(
    data=df[which(j)[is_k], ], 
    col="gold", shape=16, size=0) +
    ggtitle("k-nearest neighbors")
p2 <- p0 + geom_point(
    data=df[which(j)[is_r], ], 
    col="gold", shape=16, size=0) +
    ggtitle("fixed-radius search")
(p1 | p2) + plot_layout(nrow=1) & theme_xy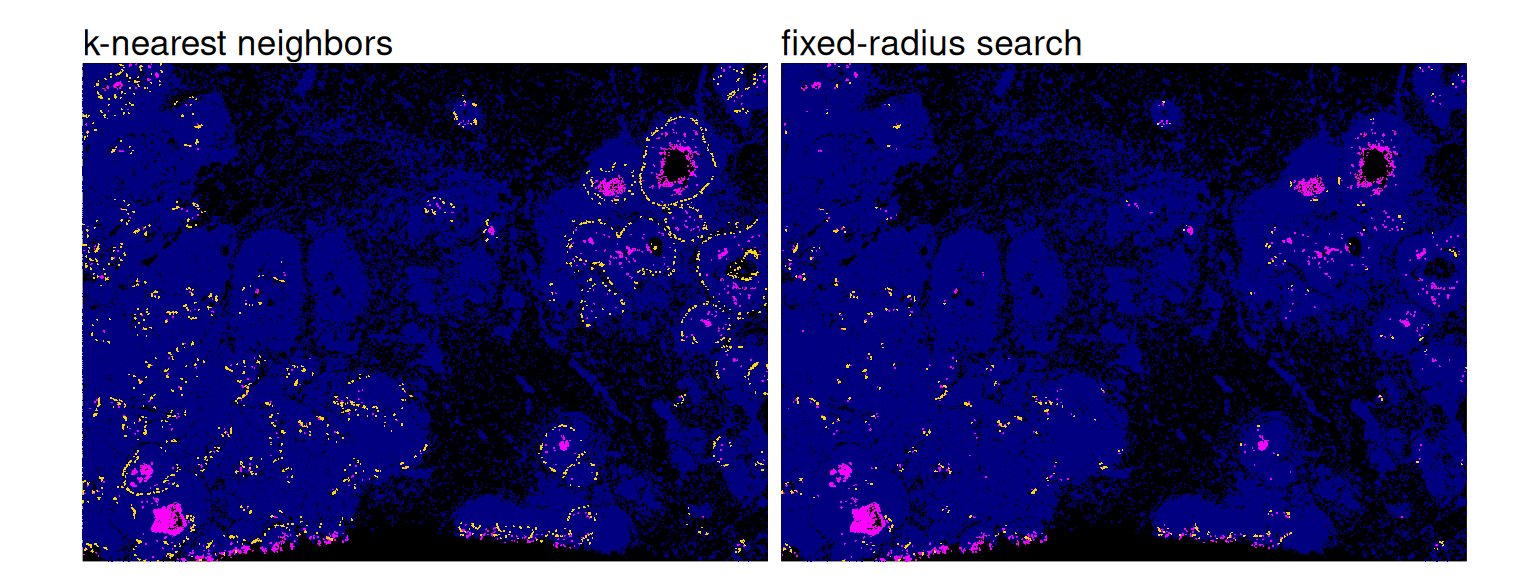

Results of kNN searches. Left: basic kNN search, highlighting source (pink) and target cells (gold). Right: kNN search with same k, but thresholding on neighbor distances.

exhaustive fixed-radius search

Note that, we could also set a very large k in order to identify all neighbors within a radius r. In order to prevent unnecessarily costly searches, it is sensible to estimate how many neighbors we would expect, and to set k accordingly. nn2() will otherwise find each cells’ \(k\)NNs, and set the indices of those with a distance \(>r\) to 0.

As an exemplary approach, we here sample 1,000 cells to estimate the highest number of NNs obtained, considering half of all target cells as potential NNs:

Code

# test search
.i <- sample(which(i), 1e3)
ns <- nn2(
    xy[j, ], xy[.i, ], 
    k=round(sum(j)/2), 
    searchtype="radius", r=r)
(.k <- max(rowSums(ns$nn.idx > 0)))

##  [1] 40

For our actual search, we then set k to be twice our estimate. As a final spot-check, we make sure that all cells have fewer than k NNs, since we might otherwise be missing some.

Code

# real search
ns <- nn2(
    xy[j, ], xy[i, ], 
    k=k <- ceiling(2*.k), 
    searchtype="radius", r=r)
max(rowSums(ns$nn.idx > 0)) < k

##  [1] TRUE

18.3 Spatial contexts

Spatial niche analysis aims at identifying regions of homogeneous composition by grouping cells based on their microenvironment. To this end, methods such as imcRtools (Windhager et al. 2023) rely on a \(k\)-nearest-neighbor (\(k\)NN) graph (based on Euclidean cell-to-cell distances), and clustering cells using common clustering algorithms (according to their neighborhood’s subpopulation frequencies).

Here, we demonstrate how to identify spatial contexts based on \(k\)-means clustering on cluster frequencies among (Euclidean) \(k\)NNs. We recommend readers consult imcRtools’ documentation for a much wider range of visualizations and downstream analyses in this context.

Code

library(imcRtools)
# construct kNN-graph based on Euclidean distances
sqe <- buildSpatialGraph(spe, 
    coords=spatialCoordsNames(spe),
    img_id="sample_id", type="knn", k=10)
# compute cluster frequencies among each cell's kNNs
sqe <- aggregateNeighbors(sqe, 
    colPairName="knn_interaction_graph", 
    aggregate_by="metadata", count_by="k")
# view composition of 1st cell's kNNs
unlist(sqe$aggregatedNeighbors[1, ])

##    1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16 
##  0.3 0.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

Code

# cluster cells by neighborhood compositions
ctx <- kmeans(sqe$aggregatedNeighbors, centers=5)
table(sqe$ctx <- factor(ctx$cluster))

##  
##      1     2     3     4     5 
##  15131 27348 48255 20479 29055

Let’s quickly view the subpopulation composition of each spatial context:

Code

df <- data.frame(spatialCoords(sqe), colData(sqe))
round(100*with(df, prop.table(table(k, ctx), 2)), 2)

##      ctx
##  k        1     2     3     4     5
##    1   0.09 36.31  2.41  0.24  0.10
##    2   0.73  2.70  5.79  1.22  0.13
##    3   0.00  4.82  3.68  0.00  0.00
##    4   0.00  6.75  7.24  0.00  0.17
##    5   2.93  0.57 16.01  4.82  6.53
##    6   2.80  0.39 13.81  5.27 15.00
##    7  45.76  0.10  1.45 63.40  0.71
##    8   1.56  1.45  7.61  2.83 11.30
##    9  42.85  0.05  0.18 16.37  0.07
##    10  1.99  0.76 23.02  3.53  7.93
##    11  0.98  0.07  9.70  1.86 42.12
##    12  0.20  0.03  5.22  0.33  5.24
##    13  0.07  0.01  0.86  0.08  0.44
##    14  0.01  0.00  1.83  0.03  8.89
##    15  0.00 45.99  0.73  0.00  0.00
##    16  0.05  0.01  0.46  0.01  1.37

Secondly, let’s visualize the obtained spatial contexts in space:

Code

pal_k <- unname(pals::trubetskoy(nlevels(df$k)))
pal_c <- c("blue", "cyan", "gold", "magenta", "maroon")
ggplot(df, aes(x_centroid, y_centroid, col=k)) + 
    scale_color_manual(values=pal_k) +
ggplot(df, aes(x_centroid, y_centroid, col=ctx)) + 
    scale_color_manual(values=pal_c) +
plot_layout(nrow=1) &
    geom_point(shape=16, size=0) &
    guides(col=guide_legend(override.aes=list(size=2))) &
    theme_xy & theme(legend.key.size=unit(0.5, "lines"))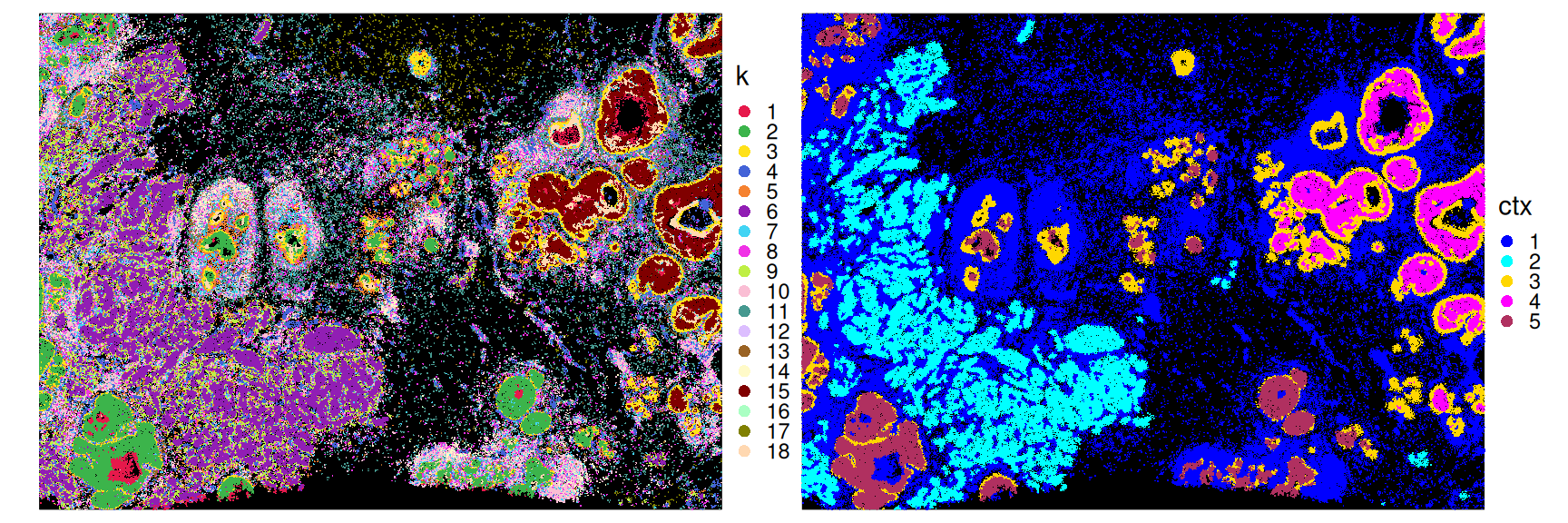

Tissue plot with cells colored by cluster (left) and spatial context (right) based on \(k\)-means clustering of cluster frequencies among each cell’s (Euclidean) \(k\)NNs.

18.4 Co-localization

hoodscanR (Liu et al. 2024) also relies on a (Euclidean) \(k\)NN graph to estimate the probability of each cell associating with its NNs. The resulting probability matrix (rows=cells, columns=NNs) can, in turn, be used to assess co-occurrence of subpopulations.

Code

library(hoodscanR)
sqe <- readHoodData(spe, anno_col="k")
nbs <- findNearCells(sqe, k=100)
mtx <- scanHoods(nbs$distance)      
grp <- mergeByGroup(mtx, nbs$cells) 
sqe <- mergeHoodSpe(sqe, grp)

To perform neighborhood co-localization analysis, plotColocal() computes the Pearson correlation of probability distribution between cells. Here, high/low values indicate attraction/repulsion between clusters:

Code

library(pheatmap)
cor <- plotColocal(sqe, pm_cols=colnames(grp), return_matrix=TRUE)
pal <- colorRampPalette(rev(hcl.colors(9, "Roma")))(100)
pheatmap(cor, 
    cellwidth=15, cellheight=15, 
    treeheight_row=5, treeheight_col=5,
    col=pal, breaks=seq(-1, 1, length=100))

measuring local mixing

Downstream, calcMetrics() can be used to calculate cell-level entropy and perplexity, which both measure the mixing of cellular neighborhoods. Here, low/high values indicate heterogeneity/homogeneity of a cell’s local neighborhood:

Code

sqe <- calcMetrics(sqe, pm_cols=colnames(grp))

Code

df <- data.frame(colData(sqe), k=spe$k, spatialCoords(spe))
vs <- c("perplexity", "entropy")
fd <- df |>
    mutate(across(all_of(vs), scale)) |>
    pivot_longer(all_of(vs)) |>
    # threshold at 2 SDs for clearer visualization
    mutate(value=case_when(abs(value) > 2 ~ sign(value)*2, TRUE ~ value))
ggplot(fd, aes(x_centroid, y_centroid, col=value)) +
    facet_grid(~name) + geom_point(shape=16, size=0) + 
    theme_xy + theme(legend.key.size=unit(0.5, "lines")) +
    scale_color_gradient2("z-scaled\nvalue", low="cyan", mid="navy", high="magenta")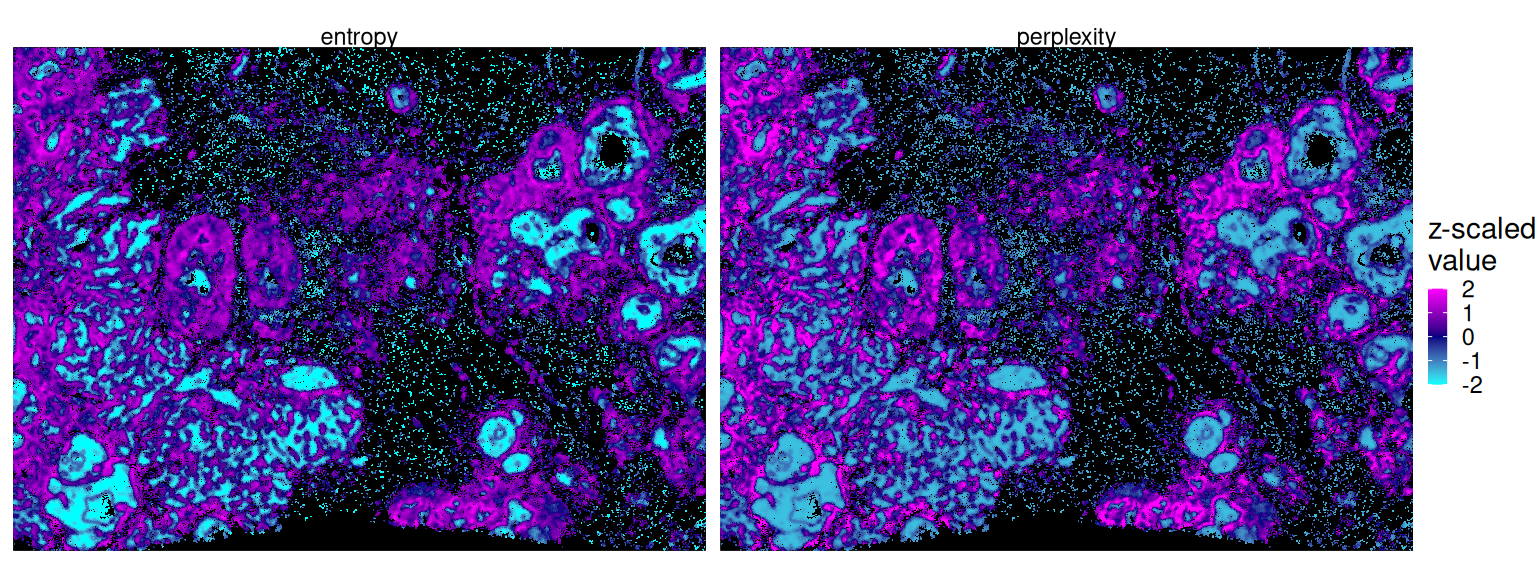

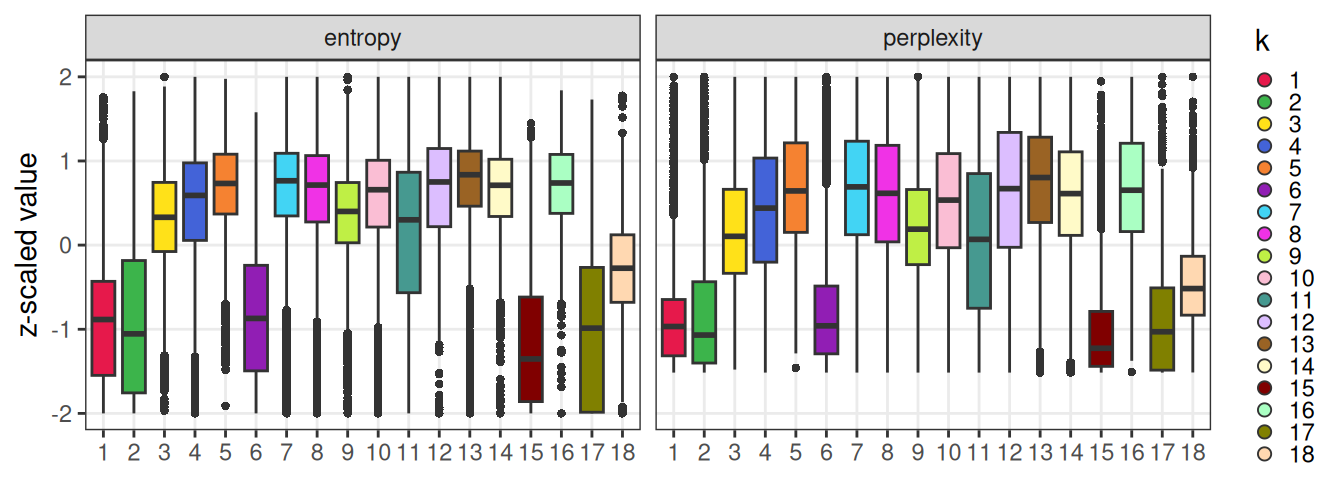
Tissue plots with cells colored by entropy and perplexity, z-scaled across cells (capped at 2 SDs).

Stratifying these values by subpopulation, we can observe that clusters forming distinct aggregates in space are lowest in entropy/perplexity (i.e., the most homogeneous locally):

Code

ggplot(fd, aes(k, value, fill=k)) +
    facet_wrap(~name) + 
    scale_fill_manual(values=pal_k) + 
    geom_boxplot(outlier.stroke=0, key_glyph="point") +
    scale_y_continuous("z-scaled value", limits=c(-2, 2)) +
    guides(fill=guide_legend(override.aes=list(shape=21, size=2))) +
    theme_bw() + theme(
        axis.title.x=element_blank(),
        panel.grid.minor=element_blank(),
        legend.key.size=unit(0.5, "lines"))

Boxplot of entropy and perplexity, stratified by cluster assignment and z-scaled across cells (capped at 2 SDs).

18.5 Appendix

References

Liu, Ning, Jarryd Martin, Dharmesh D. Bhuva, Jinjin Chen, Mengbo Li, Samuel C. Lee, Malvika Kharbanda, et al. 2024. “hoodscanR: Profiling Single-Cell Neighborhoods in Spatial Transcriptomics Data.” bioRxiv. https://doi.org/10.1101/2024.03.26.586902.

Windhager, Jonas, Vito Riccardo Tomaso Zanotelli, Daniel Schulz, Lasse Meyer, Michelle Daniel, Bernd Bodenmiller, and Nils Eling. 2023. “An End-to-End Workflow for Multiplexed Image Processing and Analysis.” Nature Protocols 18 (11): 3565–3613.