33  Structure-based analysis

33.1 Preamble

33.1.1 Introduction

Spatial omics data allow us to quantify various features that are related to tissue architecture. This allows us to perform comparisons of anatomical structure-derived features. We will refer to this type of analysis as structure-based analysis.

We will use the sosta package (Gunz, Crowell, and Robinson 2025) to reconstruct and quantify pancreatic islets from human donors suffering different stages of diabetic type 1 (T1D) and healthy controls (Damond et al. 2019). We will then compare some of the features between conditions.

33.1.2 Dependencies

Code
library(sf)
library(osfr)
library(lme4)
library(dplyr)
library(tidyr)
library(sosta)
library(ggplot2)
library(lmerTest)
library(ggfortify)
library(ExperimentHub)
library(SpatialExperiment)
# set seed for random number generation
# in order to make results reproducible
set.seed(8048)

33.1.3 Load data

An assay-free version of the dataset is available through our OSF repository (used here to reduce runtime as the following analyses do not require assay data):

Code
# load data from OSF repository (for smaller download)
osf_repo <- osf_retrieve_node("https://osf.io/5n4q3/")
osf_files <- osf_ls_files(osf_repo, 
    path="zzz", n_max=Inf,
    pattern="Damond_noAssays.rds")
dir.create(td <- tempfile())
foo <- osf_download(osf_files, path=td)
spe <- readRDS(file.path(td, list.files(td, ".rds")))
table(spe$patient_id, spe$patient_stage)
##        
##         Long-duration Non-diabetic  Onset
##    6089         91634            0      0
##    6126             0       158693      0
##    6134             0       181609      0
##    6180        141450            0      0
##    6228             0            0 142106
##    6264        146123            0      0
##    6278             0       185399      0
##    6362             0            0 202272
##    6380             0            0 129456
##    6386             0       127350      0
##    6414             0            0 166052
##    6418        104830            0      0

33.2 Visualize data

First, we plot a few selected fields of view (FOVs).

Code
# subset to 4 randomly selected FOVs
fov <- sample(unique(spe$image_name), 4)
sub <- spe[, spe$image_name %in% fov]
##  Loading required namespace: GenomeInfoDb
Code
df <- data.frame(colData(sub), spatialCoords(sub))
# visualize annotations
ggplot(df, aes(cell_x, cell_y, color=cell_category)) + 
    geom_point(size=0.4) + facet_wrap(~image_name, ncol=2) + 
    scale_color_manual(values=unname(pals::okabe(n=5))) +
    guides(col=guide_legend(override.aes=list(size=2))) +
    coord_equal() + theme_classic()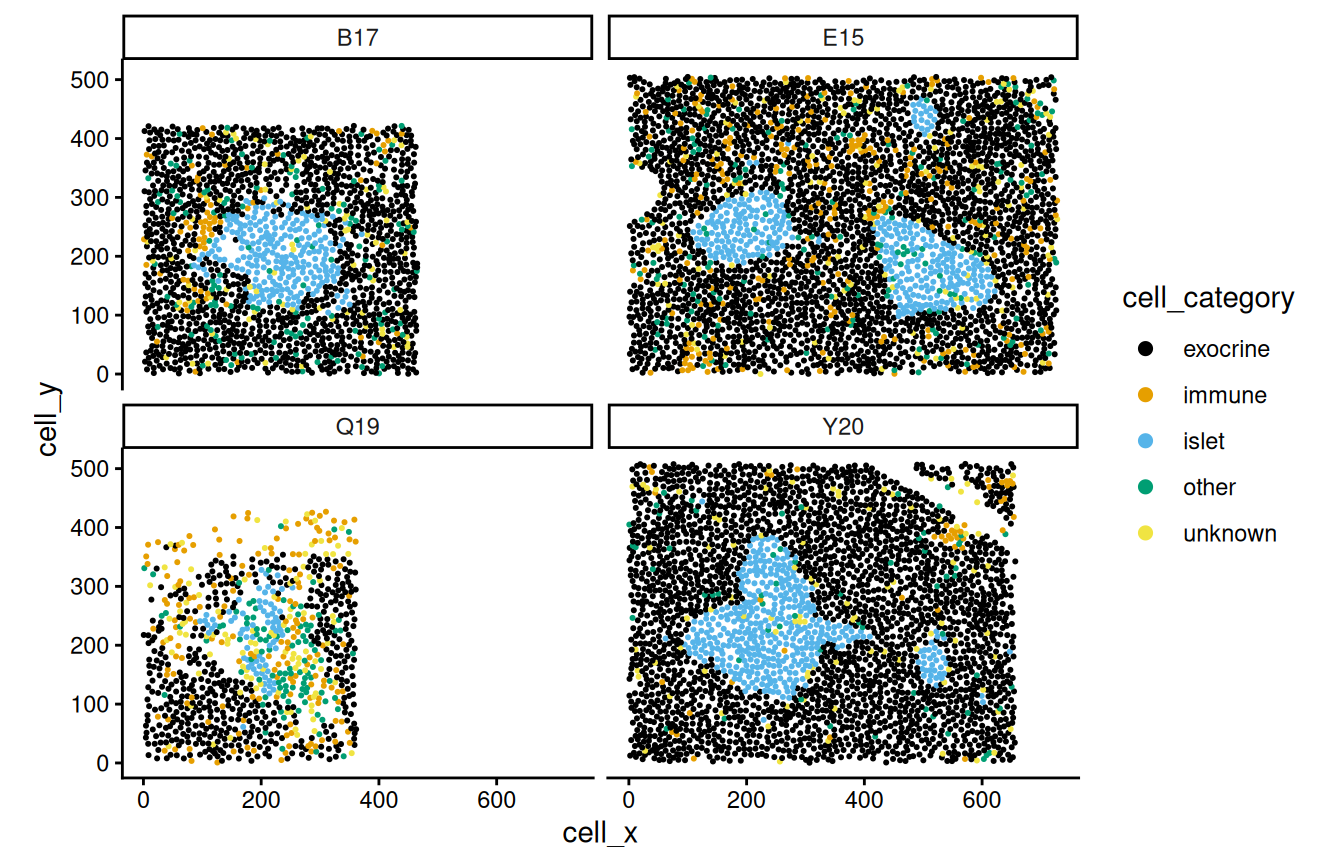

33.3 Islet reconstrution

Next, we will reconstruct or segment the individual islets using a density-based approach implemented in sosta.

Code
# use 'nImages' randomly samples 
# images for parameter estimation
est <- estimateReconstructionParametersSPE(
    spe, 
    marks="cell_category", 
    imageCol="image_name", 
    markSelect="islet", 
    nImages=10, 
    nCores=4, 
    plotHist=FALSE)
# get parameter estimates for ...
th <- mean(est$thres) # threshold
bw <- mean(est$bndw)  # bandwidth

The sosta package uses a reconstruction method based on the point pattern density of the islet cells. This method needs two parameters:

  • a bandwidth that is used for intensity profile estimation, and
  • a threshold based on which the islets are reconstructed.
Code
shapeIntensityImage(
    spe, 
    marks="cell_category", 
    imageCol="image_name", 
    imageId=fov[4], 
    markSelect="islet")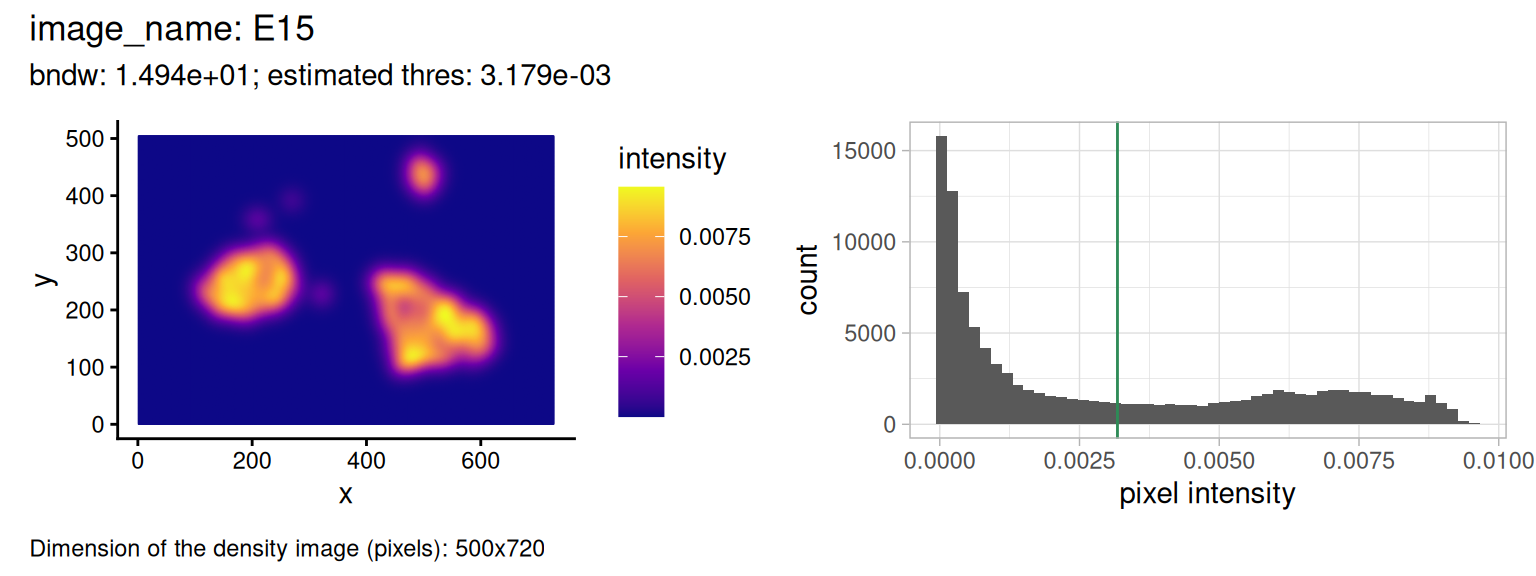

Shown on the left is a density (pixel-level) image, and on the right a histogram of the intensity values. The method selects every pixel above a certain threshold for reconstruction. The smoothing bandwidth that generates the image is estimated using cross-validation (see function bw.diggle() of the spatstat.explore package from CRAN).

The threshold is estimated by taking the mean between the two modes of the (truncated) pixel intensity distribution. The function estimateReconstructionParametersSPE() repeats the estimation of these parameters for a selection of images in the dataset.

To make the reconstruction comparable between images we then use a fixed set of parameters for all images, in our case the mean of the individual parameters for a subset of the dataset.

Code
allIslets <- reconstructShapeDensitySPE(
    spe, 
    marks="cell_category", 
    imageCol="image_name", 
    markSelect="islet", 
    bndw=bw, 
    thres=th, 
    nCores=4)

Now we can inspect the reconstruction in the sample images.

Code
# subset to selected FOVs
subIslets <- allIslets[allIslets$image_name %in% fov, ]
# visualize annotations 
ggplot(df, aes(cell_x, cell_y, color=cell_category)) + 
    geom_point(size=0.4) + facet_wrap(~image_name, ncol=2) + 
    scale_color_manual(values=unname(pals::okabe(n=5))) +
    guides(col=guide_legend(override.aes=list(size=2))) +
    coord_equal() + theme_classic() +
    geom_sf( # geom for structure outlines
        data=subIslets, inherit.aes=FALSE, 
        color="red", fill=NA, linewidth=1)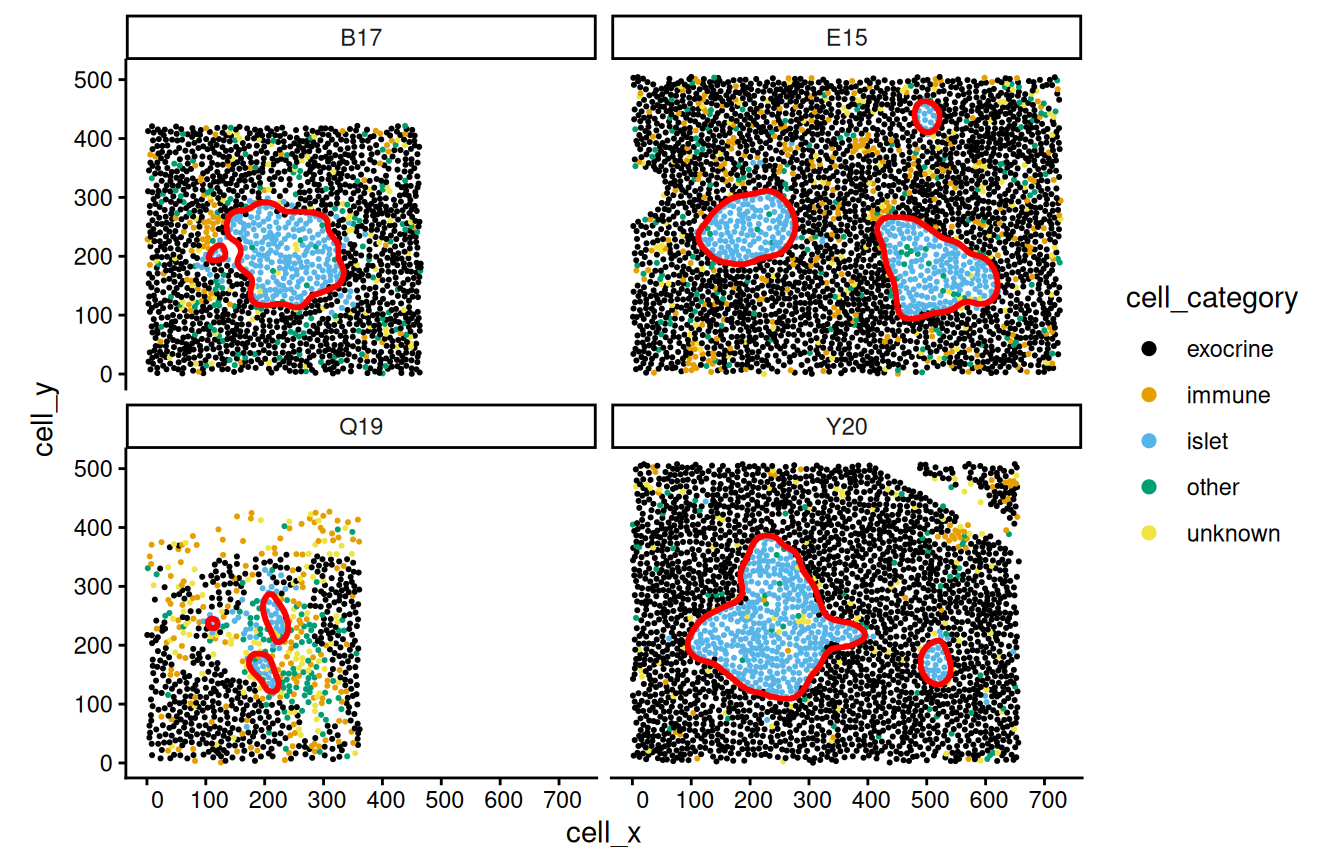

The allIslets object is a simple feature collection which contains polygons (<GEOMETRY> column), a structure identifier (structID), and the image identifier (image_name). We will add some patient metadata to the object.

Code
# factor levels for 'patient_stage'
lv <- c("Non-diabetic", "Onset", "Long-duration")
# cell metadata columns to keep
colsKeep <- c(
    "sample_id", "image_name",
    "patient_disease_duration", 
    "patient_id", "patient_stage", 
    "patient_age", "patient_gender",
    "tissue_slide", "tissue_region") 
patientData <- colData(spe) |> 
    as_tibble() |> 
    # keep selected columns
    select(all_of(colsKeep)) |> 
    # refactor patient IDs & stages
    group_by(image_name) |> 
    mutate_at("patient_id", factor) |>
    mutate_at("patient_stage", factor, lv) |>
    # keep only unique combinations
    unique() 
# join with results from reconstruction
allIslets <- left_join(allIslets, patientData, by="image_name")

33.4 Quantification of geometric features

Now we can proceed with quantification of geometric aspects of the islets, and combine them with patient information.

Code
isletMetrics <- totalShapeMetrics(allIslets)
allIslets <- cbind(allIslets, t(isletMetrics))

PCA can give us an overview of the different features; here, each dot represents one structure.

Code
pca <- prcomp(t(isletMetrics), scale.=TRUE)
autoplot(pca, 
    x=1, y=2, 
    data=allIslets,
    color="patient_stage", 
    size=2, 
    loadings=TRUE, 
    loadings.colour="steelblue3", 
    loadings.label=TRUE, 
    loadings.label.size=3, 
    loadings.label.repel=TRUE, 
    loadings.label.colour="black") +
    theme_bw() + coord_fixed() + 
    scale_color_manual(values=unname(pals::tol(n=3)))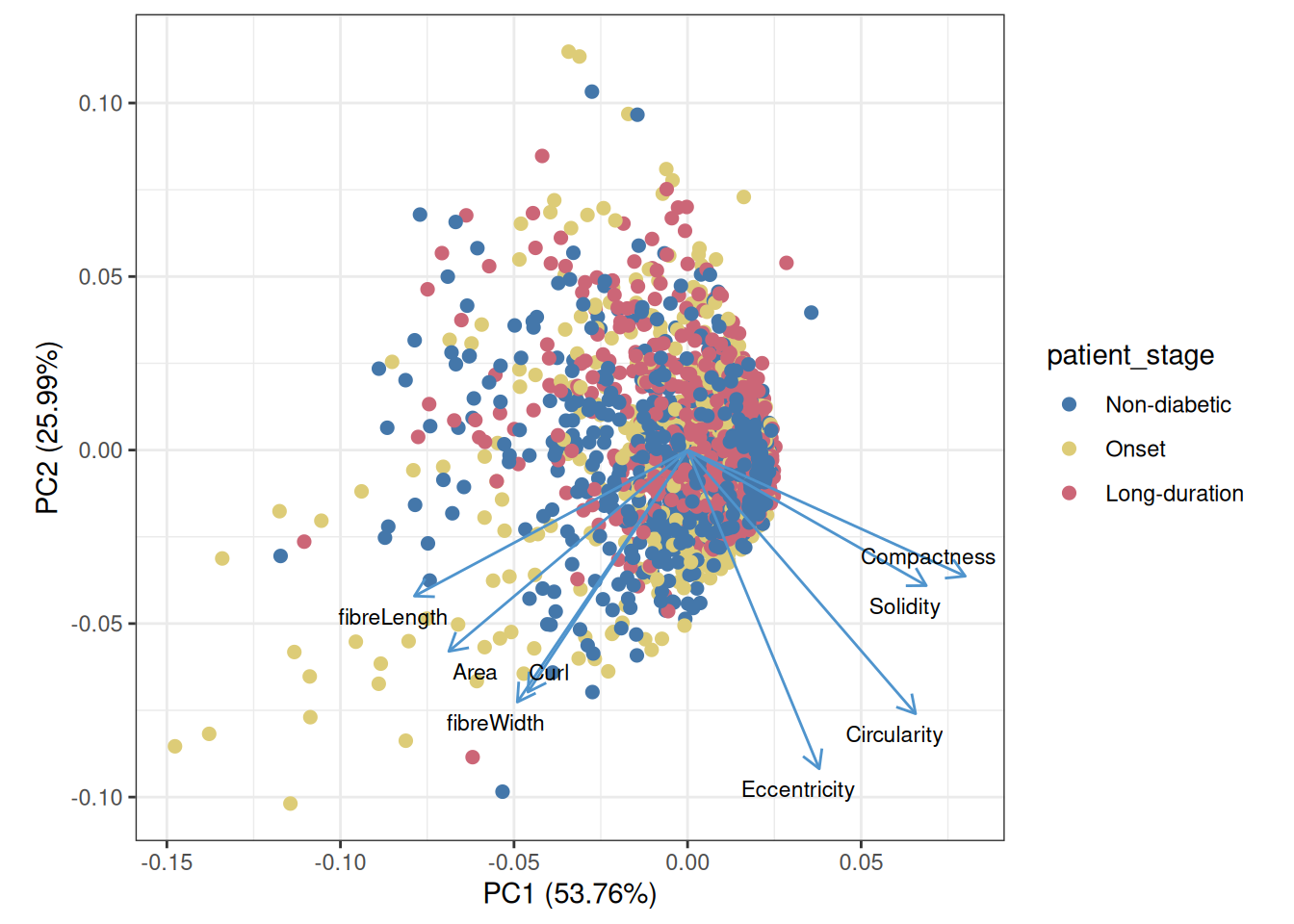

Code
# wrangling
df <- allIslets |> 
    st_drop_geometry() |> 
    select(patient_stage, rownames(isletMetrics)) |> 
    pivot_longer(-patient_stage) |> 
    filter(name %in% c("Area", "Compactness", "Curl"))
# visualization
ggplot(df, aes(patient_stage, value, fill=patient_stage)) + 
    geom_violin() + geom_boxplot(aes(fill=NULL), width=0.3) + 
    scale_fill_manual(values=unname(pals::tol(n=3))) +
    scale_x_discrete(guide=guide_axis(n.dodge=2)) + 
    facet_wrap(~name, scales="free") + 
    guides(fill="none") + theme_bw()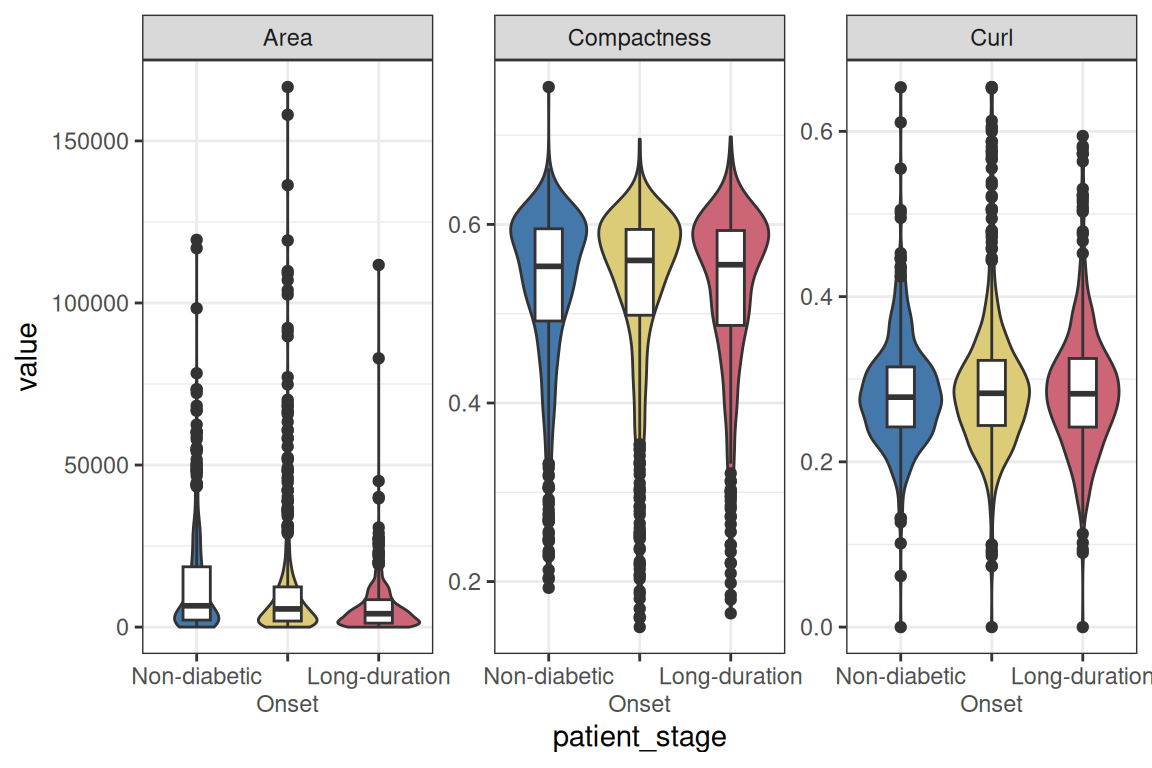

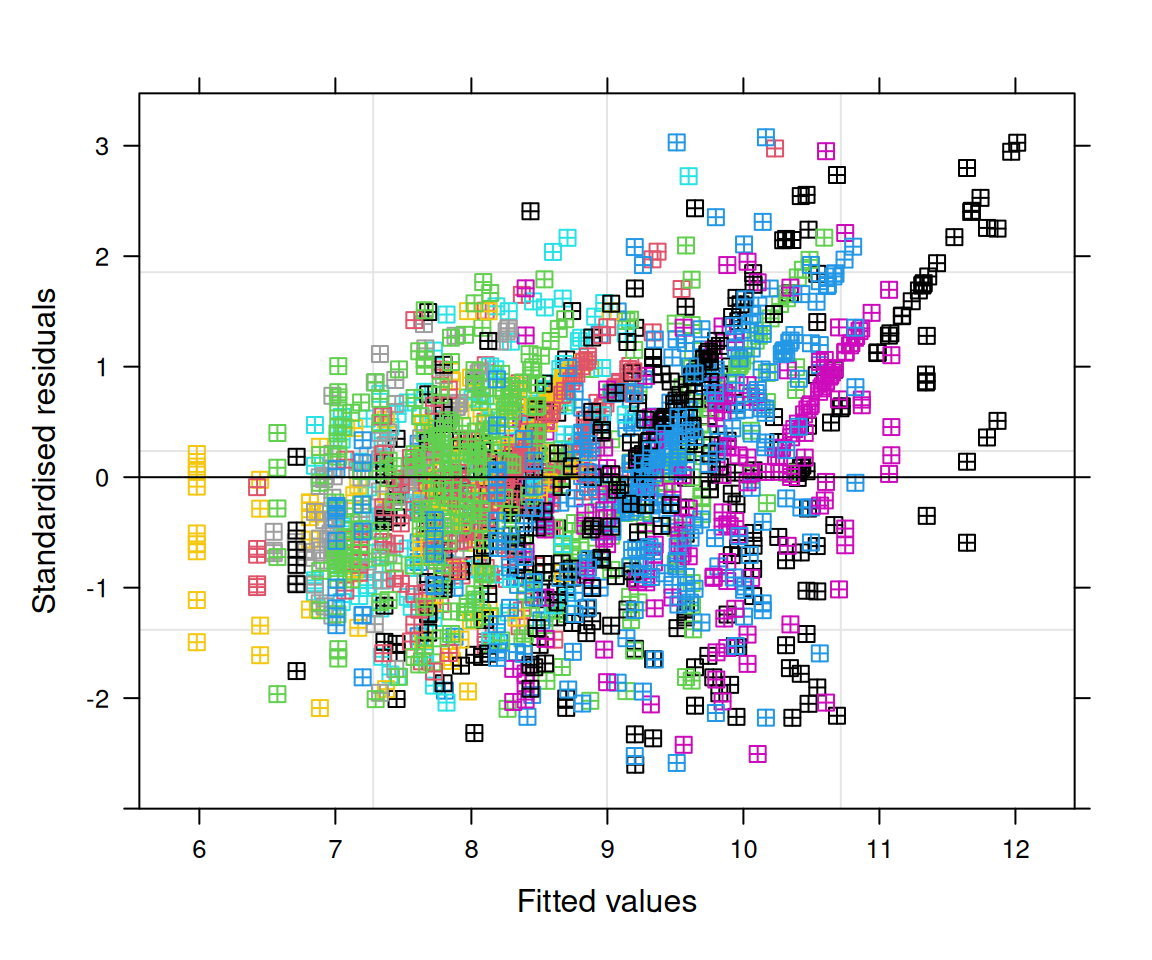
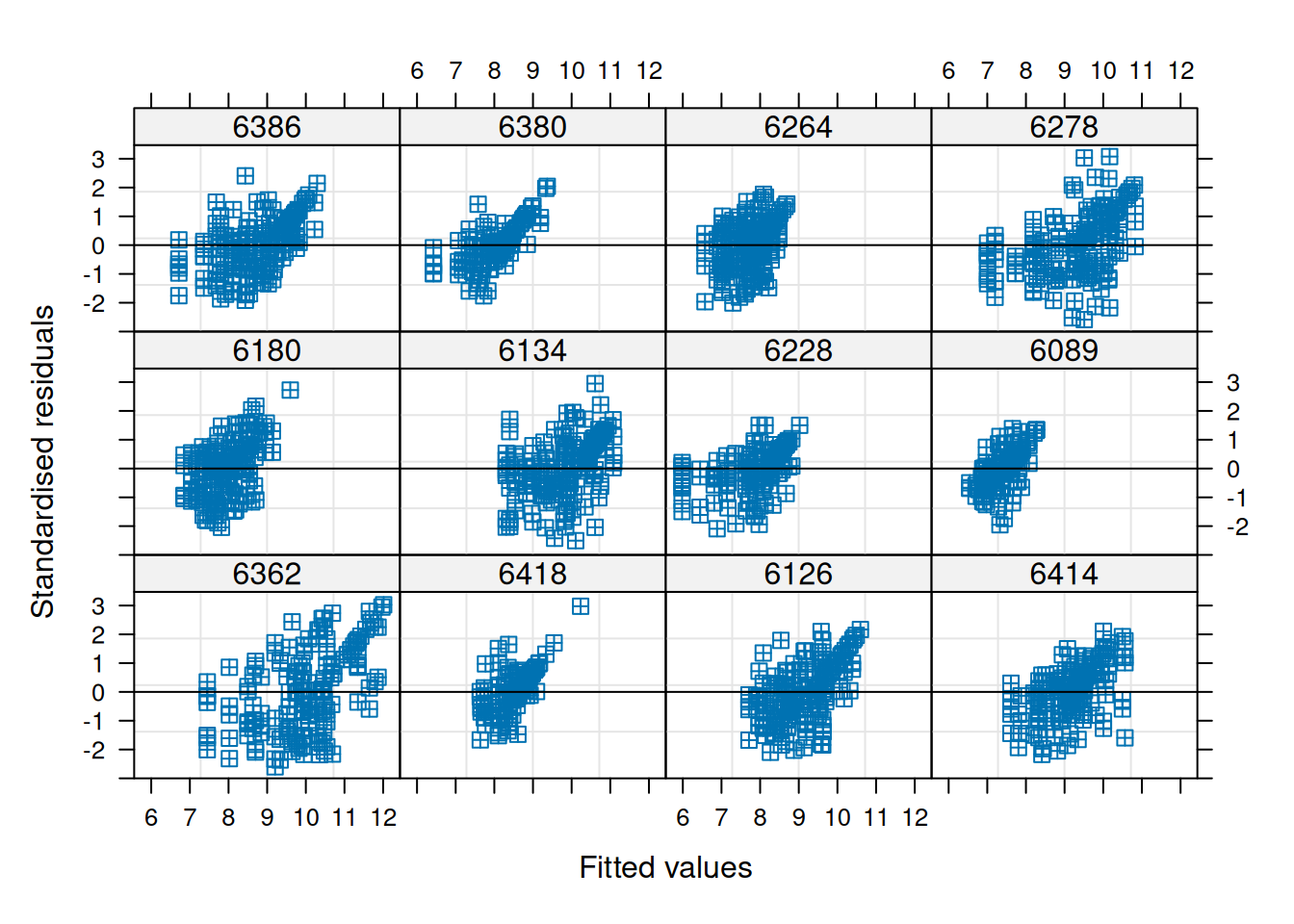
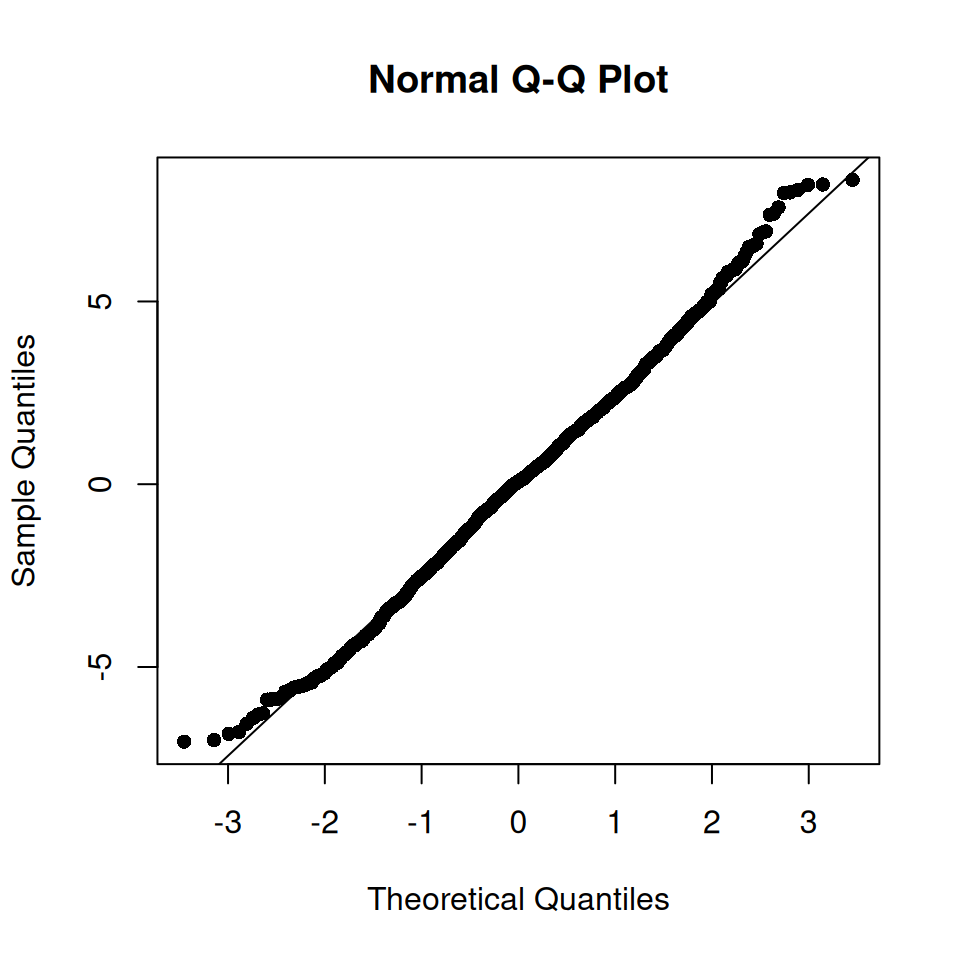
Let’s focus on the area of the islets and facet by stage to look at patient variability. As the distribution is very skewed, we will use a 1/4-power transformation on the area of the islets. The transformation was chosen after inspection of the model diagnostics (see below).

Code
# wrangling
df <- allIslets |> 
    st_drop_geometry() |> 
    select(patient_stage, patient_id, rownames(isletMetrics)) |> 
    pivot_longer(-c(patient_stage, patient_id)) |> 
    filter(name %in% c("Area"))
# visualization
ggplot(df, aes(patient_id, value^(1/4), fill=patient_stage)) + 
    geom_violin() + geom_boxplot(fill=NA, width=0.3) + 
    scale_fill_manual(values=unname(pals::tol(n=3))) +
    facet_wrap(~patient_stage, scales="free_x") + 
    geom_jitter(size=0.5) + ylab("Area") +
    guides(fill="none") + theme_bw()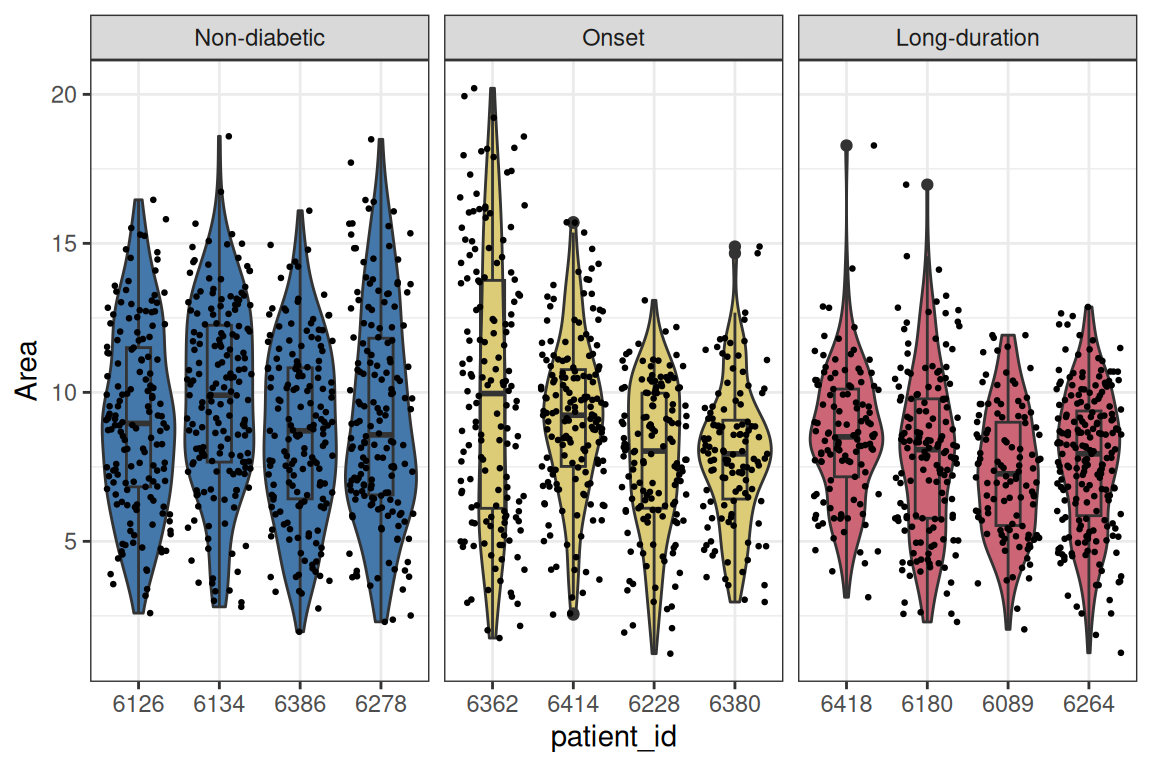

33.5 Between-sample comparison

An important aspect to note is that the individual structure metrics are not independent measurements, since there are generally repeated measurments (i.e., multiple islets) per slide and per patient. Therefore, we need to account for this correlation between measurements.

To account for this, we will use mixed linear models with random effects for the patient and the individual slides (image name). The lme4 package will be use for fitting linear mixed effects models (Bates et al. 2015) and lmerTest for p-value calculations (Kuznetsova, Brockhoff, and Christensen 2017).

Code
f <- Area^(1/4) ~ patient_stage + (1|patient_id) + (1|image_name)
summary(mod <- lmer(formula=f, data=allIslets))
##  Linear mixed model fit by REML. t-tests use Satterthwaite's method [
##  lmerModLmerTest]
##  Formula: f
##     Data: allIslets
##  
##  REML criterion at convergence: 9028
##  
##  Scaled residuals: 
##      Min      1Q  Median      3Q     Max 
##  -2.6027 -0.6199  0.0265  0.6129  3.0764 
##  
##  Random effects:
##   Groups     Name        Variance Std.Dev.
##   image_name (Intercept) 1.4628   1.2095  
##   patient_id (Intercept) 0.5426   0.7366  
##   Residual               7.3230   2.7061  
##  Number of obs: 1806, groups:  image_name, 844; patient_id, 12
##  
##  Fixed effects:
##                             Estimate Std. Error      df t value Pr(>|t|)    
##  (Intercept)                  9.5935     0.3924  8.8393  24.447 2.01e-09 ***
##  patient_stageOnset          -0.5624     0.5557  8.8860  -1.012    0.338    
##  patient_stageLong-duration  -1.5404     0.5563  8.9198  -2.769    0.022 *  
##  ---
##  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##  
##  Correlation of Fixed Effects:
##              (Intr) ptnt_O
##  ptnt_stgOns -0.706       
##  ptnt_stgLn- -0.705  0.498

From the fixed effects section in the model summary above, we note that there is a statistically significant difference in the transformed islet area of long-duration patients compared to non-diabetic patients, while the effect for onset patients is not significant at the 5% level. This result accounts for correlation at the patient and image level as modeled by random intercepts. The transformation (1/4-power) was chosen after inspection of the residual behavior in the model diagnostics for this dataset and feature of interest specifically.

Code
res <- resid(., scaled=TRUE) ~ fitted(.)
plot(mod, res, 
    pch=12, abline=0, 
    xlab="Fitted values", 
    ylab="Standardised residuals",
    col=allIslets$patient_id)

Code
res <- resid(., scaled=TRUE) ~ fitted(.) | patient_id
plot(mod, res, 
    pch=12, abline=0, 
    xlab="Fitted values", 
    ylab="Standardised residuals")

Code
qqnorm(resid(mod), pch=16)
qqline(resid(mod))

33.6 Appendix

This chapter is based on the sosta vignette “2. Reconstruction and analysis of pancreatic islets from IMC data”.

Additional packages to calculate anatomical structure-derived features include:

  • The Bioconductor packages SPIAT and imcRtools offer other functions to quantify features on the anatomical structure level. These could also be input for mixed effect modeling as illustrated above.

  • The packages vegan and poem are useful when calculating diversity metrics within structures and/or border regions. To identify border regions and how to overlap anatomical regions with sample coordinates, please have a look at the sosta vignette.

References

Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015. “Fitting Linear Mixed-Effects Models Using Lme4.” Journal of Statistical Software 67: 1–48. https://doi.org/10.18637/jss.v067.i01.
Damond, Nicolas, Stefanie Engler, Vito R. T. Zanotelli, Denis Schapiro, Clive H. Wasserfall, Irina Kusmartseva, Harry S. Nick, et al. 2019. “A Map of Human Type 1 Diabetes Progression by Imaging Mass Cytometry.” Cell Metabolism 29: 755–68. https://doi.org/10.1016/j.cmet.2018.11.014.
Gunz, Samuel, Helena L. Crowell, and Mark D. Robinson. 2025. “Analysis of Anatomical Multi-Cellular Structures from Spatial Omics Data Using Sosta.” bioRxiv. https://doi.org/10.1101/2025.10.13.682065.
Kuznetsova, Alexandra, Per B. Brockhoff, and Rune H. B. Christensen. 2017. “lmerTest Package: Tests in Linear Mixed Effects Models.” Journal of Statistical Software 82: 1–26. https://doi.org/10.18637/jss.v082.i13.
Back to top