20 Neighborhood analysis

20.1 Preamble

20.1.1 Introduction

Neighborhood analysis aims to investigate the composition of and interaction between cells and cell types within small regions of tissue, which are referred to as neighborhoods or niches.

20.1.2 Dependencies

Code

library(dplyr)
library(tidyr)
library(ggplot2)
library(patchwork)
library(RColorBrewer)
library(BiocParallel)
library(SpatialExperiment)

Code

# load data from previous section
spe <- readRDS("img-spe_cl.rds")
spe$k <- colLabels(spe)

Code

# basic theme for spatial plots
theme_xy <- list(
    coord_equal(expand=FALSE), 
    theme_void(), theme(
        plot.margin=margin(l=5),
        legend.key=element_blank(),
        panel.background=element_rect(fill="black")))

20.2 Nearest neighbors

Custom spatial analyses may rely on identifying nearest neighbors (NNs) of cells. We recommend RANN for this purpose, which finds NNs in \(O(N\log N)\) time for \(N\) cells (c.f., conventional approaches would take \(O(N^2)\) time) by relying on a Approximate Near Neighbor (ANN) C++ library. Furthermore, there is support for exact, approximate, and fixed-radius searchers. The latter is of particular interest in biology; e.g., one might require \(k\)NNs to lie within a biologically sensible distance as to avoid consideration of cells that are far-off, especially in sparse regions or at tissue borders.

As a toy example, we here compute the \(k\)NNs between a pair of subpopulations, with and without thresholding on NN distances (searchtype="radius").

For the first approach, each cell will receive \(k\) neighbors exactly,
but these may lie within an arbitrary distance.
For the second approach, cells will receive \(\leq k\) neighbors,
depending on how many cells lie within a radius \(r\).

Code

library(RANN)
k <- 10 # num. neighbors
r <- 50 # dist. threshold
i <- spe$k == 1 # source
j <- spe$k == 4 # target
xy <- spatialCoords(spe)
# k-NN search: all cells have k neighbors
ns_k <- nn2(xy[j, ], xy[i, ], k=k)
is_k <- ns_k$nn.idx
all(rowSums(is_k > 0) == k) 
# w/ fixed-radius: cells have 0-k neighbors
ns_r <- nn2(xy[j, ], xy[i, ], k=k, searchtype="radius", r=r)
is_r <- ns_r$nn.idx
range(rowSums(is_r > 0))

##  [1] TRUE
##  [1]  0 10

The neighbors obtained via fixed-radius search (right) are less scattered than those obtained for unlimited distances (left); the former are arguably more meaningful in a biological context:

Code

df <- data.frame(xy, colData(spe))
p0 <- ggplot(df, aes(x_centroid, y_centroid)) + 
    geom_point(data=df, col="navy", shape=16, size=0) +
    geom_point(data=df[i, ], col="magenta", shape=16, size=0) 
p1 <- p0 + geom_point(
    data=df[which(j)[is_k], ], 
    col="gold", shape=16, size=0) +
    ggtitle("k-nearest neighbors")
p2 <- p0 + geom_point(
    data=df[which(j)[is_r], ], 
    col="gold", shape=16, size=0) +
    ggtitle("fixed-radius search")
(p1 | p2) + plot_layout(nrow=1) & theme_xy

Results of kNN searches. Left: basic kNN search, highlighting source (pink) and target cells (gold). Right: kNN search with same k, but thresholding on neighbor distances.

exhaustive fixed-radius search

Note that, we could also set a very large k in order to identify all neighbors within a radius r. In order to prevent unnecessarily costly searches, it is sensible to estimate how many neighbors we would expect, and to set k accordingly. nn2() will otherwise find each cells’ \(k\)NNs, and set the indices of those with a distance \(>r\) to 0.

As an exemplary approach, we here sample 1,000 cells to estimate the highest number of NNs obtained, considering half of all target cells as potential NNs:

Code

# test search
.i <- sample(which(i), 1e3)
ns <- nn2(
    xy[j, ], xy[.i, ], 
    k=round(sum(j)/2), 
    searchtype="radius", r=r)
(.k <- max(rowSums(ns$nn.idx > 0)))

##  [1] 34

For our actual search, we then set k to be twice our estimate. As a final spot-check, we make sure that all cells have fewer than k NNs, since we might otherwise be missing some.

Code

# real search
ns <- nn2(
    xy[j, ], xy[i, ], 
    k=k <- ceiling(2*.k), 
    searchtype="radius", r=r)
max(rowSums(ns$nn.idx > 0)) < k

##  [1] TRUE

20.3 Spatial contexts

Spatial niche analysis aims at identifying regions of homogeneous composition by grouping cells based on their microenvironment. To this end, methods such as imcRtools (Windhager et al. 2023) rely on a \(k\)-nearest-neighbor (\(k\)NN) graph (based on Euclidean cell-to-cell distances), and clustering cells using common clustering algorithms (according to their neighborhood’s subpopulation frequencies).

Here, we demonstrate how to identify spatial contexts based on \(k\)-means clustering on cluster frequencies among (Euclidean) \(k\)NNs. We recommend readers consult the imcRtools documentation for a much wider range of visualizations and downstream analyses in this context.

Code

library(imcRtools)
# construct kNN-graph based on Euclidean distances
sqe <- buildSpatialGraph(spe, 
    coords=spatialCoordsNames(spe),
    img_id="sample_id", type="knn", k=10)
# compute cluster frequencies among each cell's kNNs
sqe <- aggregateNeighbors(sqe, 
    colPairName="knn_interaction_graph", 
    aggregate_by="metadata", count_by="k")
# view composition of 1st cell's kNNs
unlist(sqe$aggregatedNeighbors[1, ])

##    1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16 
##  0.3 0.7 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

Code

# cluster cells by neighborhood compositions
ctx <- kmeans(sqe$aggregatedNeighbors, centers=5)
table(sqe$ctx <- factor(ctx$cluster))

##  
##      1     2     3     4     5 
##  35383 48397 29069 12537 14882

Let’s quickly view the subpopulation composition of each spatial context:

Code

df <- data.frame(spatialCoords(sqe), colData(sqe))
round(100*with(df, prop.table(table(k, ctx), 2)), 2)

##      ctx
##  k        1     2     3     4     5
##    1   0.17  1.55  0.08 82.01  0.48
##    2   1.00  5.75  0.12  3.39  2.24
##    3   0.00  4.17  0.00  1.72  5.80
##    4   0.00  6.91  0.16  8.64  6.12
##    5   3.93 16.03  6.54  0.72  0.48
##    6   4.18 13.79 15.01  0.63  0.22
##    7  56.04  1.61  0.73  0.22  0.01
##    8   2.31  7.67 11.28  1.00  1.57
##    9  27.69  0.24  0.09  0.12  0.00
##    10  2.81 22.94  7.92  1.18  0.64
##    11  1.46  9.67 42.13  0.10  0.07
##    12  0.27  5.20  5.24  0.04  0.01
##    13  0.07  0.86  0.45  0.01  0.01
##    14  0.02  1.82  8.89  0.01  0.00
##    15  0.00  1.34  0.00  0.22 82.35
##    16  0.03  0.46  1.37  0.01  0.00

Secondly, let’s visualize the obtained spatial contexts in space:

Code

pal_k <- unname(pals::trubetskoy(nlevels(df$k)))
pal_c <- c("blue", "cyan", "gold", "magenta", "maroon")
ggplot(df, aes(x_centroid, y_centroid, col=k)) + 
    scale_color_manual(values=pal_k) +
ggplot(df, aes(x_centroid, y_centroid, col=ctx)) + 
    scale_color_manual(values=pal_c) +
plot_layout(nrow=1) &
    geom_point(shape=16, size=0) &
    guides(col=guide_legend(override.aes=list(size=2))) &
    theme_xy & theme(legend.key.size=unit(0.5, "lines"))

Tissue plot with cells colored by cluster (left) and spatial context (right) based on \(k\)-means clustering of cluster frequencies among each cell’s (Euclidean) \(k\)NNs.

20.4 Co-localization

hoodscanR (Liu et al. 2025) also relies on a (Euclidean) \(k\)NN graph to estimate the probability of each cell associating with its NNs. The resulting probability matrix (rows=cells, columns=NNs) can, in turn, be used to assess co-occurrence of subpopulations.

Code

library(hoodscanR)
sqe <- readHoodData(spe, anno_col="k")
nbs <- findNearCells(sqe, k=100)
mtx <- scanHoods(nbs$distance)      
grp <- mergeByGroup(mtx, nbs$cells) 
sqe <- mergeHoodSpe(sqe, grp)

To perform neighborhood co-localization analysis, plotColocal() computes the Pearson correlation of probability distribution between cells. Here, high/low values indicate attraction/repulsion between clusters:

Code

library(pheatmap)
cor <- plotColocal(sqe, pm_cols=colnames(grp), return_matrix=TRUE)
pal <- colorRampPalette(rev(hcl.colors(9, "Roma")))(100)
pheatmap(cor, 
    cellwidth=15, cellheight=15, 
    treeheight_row=5, treeheight_col=5,
    col=pal, breaks=seq(-1, 1, length=100))

measuring local mixing

Downstream, calcMetrics() can be used to calculate cell-level entropy and perplexity, which both measure the mixing of cellular neighborhoods. Here, low/high values indicate heterogeneity/homogeneity of a cell’s local neighborhood:

Code

sqe <- calcMetrics(sqe, pm_cols=colnames(grp))

Code

df <- data.frame(colData(sqe), k=spe$k, spatialCoords(spe))
vs <- c("perplexity", "entropy")
fd <- df |>
    mutate(across(all_of(vs), scale)) |>
    pivot_longer(all_of(vs)) |>
    # threshold at 2 SDs for clearer visualization
    mutate(value=case_when(abs(value) > 2 ~ sign(value)*2, TRUE ~ value))
ggplot(fd, aes(x_centroid, y_centroid, col=value)) +
    facet_grid(~name) + geom_point(shape=16, size=0) + 
    theme_xy + theme(legend.key.size=unit(0.5, "lines")) +
    scale_color_gradient2("z-scaled\nvalue", low="cyan", mid="navy", high="magenta")

Tissue plots with cells colored by entropy and perplexity, z-scaled across cells (capped at 2 SDs).

Stratifying these values by subpopulation, we can observe that clusters forming distinct aggregates in space are lowest in entropy/perplexity (i.e., the most homogeneous locally):

Code

ggplot(fd, aes(k, value, fill=k)) +
    facet_wrap(~name) + 
    scale_fill_manual(values=pal_k) + 
    geom_boxplot(outlier.stroke=0, key_glyph="point") +
    scale_y_continuous("z-scaled value", limits=c(-2, 2)) +
    guides(fill=guide_legend(override.aes=list(shape=21, size=2))) +
    theme_bw() + theme(
        axis.title.x=element_blank(),
        panel.grid.minor=element_blank(),
        legend.key.size=unit(0.5, "lines"))

Boxplot of entropy and perplexity, stratified by cluster assignment and z-scaled across cells (capped at 2 SDs).

20.5 Spatial density-based analysis

scider (Li et al. 2025) defines spatial domains as regions of interest (ROIs) while preserving the tissue structure through spatial density analysis. Kernel density estimation (KDE) is used to describe the spatial distributions of cells, and ROIs are identified based on the spatial density of some cell types of interest (COIs). One can also calculate the spatial density of transcript expression of a gene or a gene set, so that gene (set)-specific ROIs can be identified. ROIs can then be used for downstream analysis such as cell type co-localization, cell type composition and differential expression (DE) analysis. All functions operate on SpatialExperiment objects, allowing seemless integration. Using the Xenium breast carcinoma dataset, we demonstrate a standard scider workflow.

Code

library(scider)
library(OSTA.data)
library(SpatialExperimentIO)

pa <- OSTA.data_load("Xenium_HumanBreast1_Janesick")
td <- tempfile()
dir.create(td)
unzip(pa, exdir = td)
spe <- readXeniumSXE(td)

In this example, we define ROIs based on the celluar density of tumor cells, that is, DCIS_1, DCIS_2 and invasive tumor cells are considered as the COI. Firstly, we need to add cell type annotations to colData, where cell type annotations were obtained from the original publication (Janesick et al. 2023).

Code

anno <- read.csv(file.path(td, "annotation.csv"))
colData(spe)[['cell_type']] <- anno$Annotation[match(spe$cell_id, anno$Barcode)]

scider::plotSpatial(spe, group = "cell_type", pt.alpha = 1)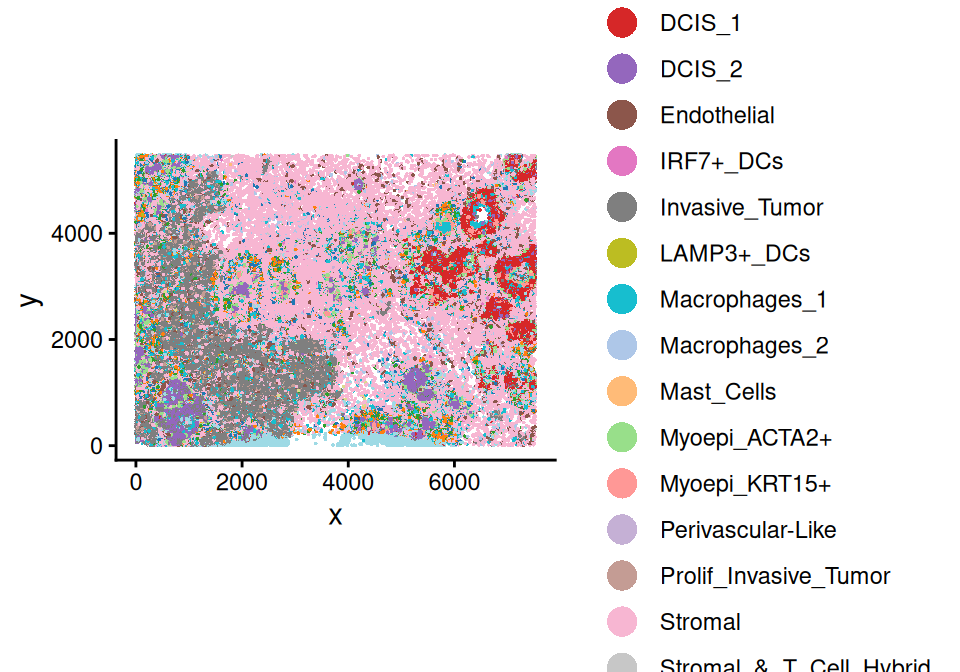

Spatial plot of the Xenium breast carcinoma sample, replicate 1.

We first estimate the spatial density of each cell type using the gridDensity() function.

Code

spe <- gridDensity(spe, grid.length.x = 50, bandwidth = 25)
metadata(spe)$grid_density[1:4, 1:8]

##  DataFrame with 4 rows and 8 columns
##       x_grid    y_grid    node_x    node_y        node density_b_cells
##    <numeric> <numeric> <numeric> <numeric> <character>       <numeric>
##  1   2.13252   1.36716         1         1         1-1    -7.00970e-17
##  2  52.13252   1.36716         2         1         2-1    -4.07403e-17
##  3 102.13252   1.36716         3         1         3-1    -6.61382e-17
##  4 152.13252   1.36716         4         1         4-1     2.35977e-16
##    density_cd4_t_cells density_cd8_t_cells
##              <numeric>           <numeric>
##  1        -2.04811e-16        -1.43713e-16
##  2        -3.60811e-16         4.88041e-11
##  3        -3.24988e-16         1.07286e-06
##  4         7.18931e-17         4.32820e-04

The density value represents the expected number of COI cells on each grid, and can be visualized by the plotDensity() function. For example, here we visualize the density of COI cells:

Code

coi <- c("DCIS_1", "DCIS_2", "Invasive_Tumor")
scider::plotDensity(spe, coi = coi, probs = 0.5) +
  ggtitle("Spatial density of tumour cells")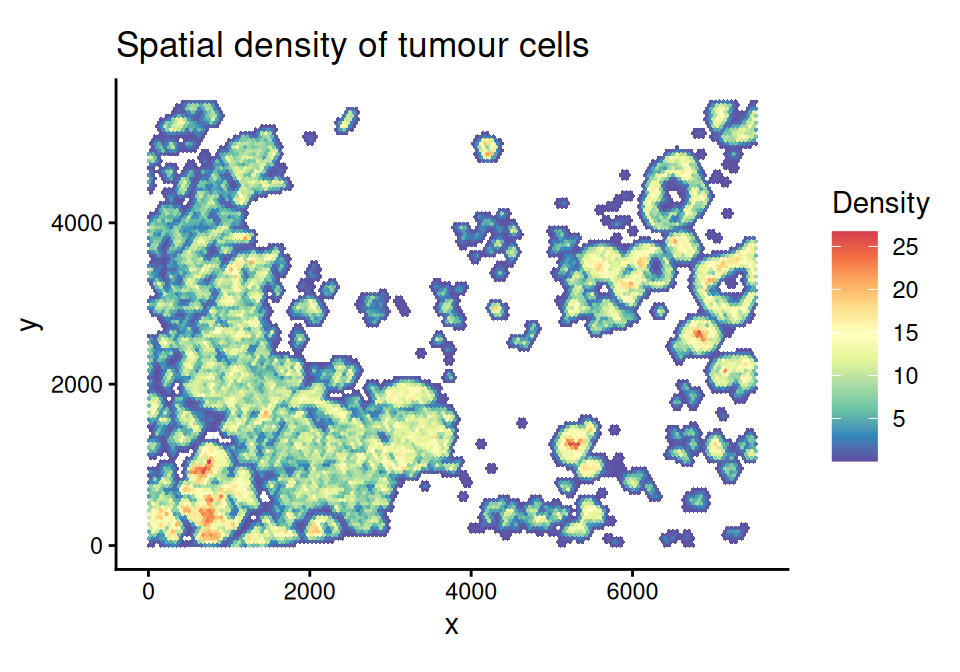

Heatmap of the spatial density of COI cells.

ROI detection is performed using a graph-based approach as described in Li et al. (2025). Only grids with \(\geq 1\) expected COI cell (estimated COI density \(\geq 1\)) are retained in ROI detection.

Code

spe <- findROI(spe, coi = coi, min.density = 1)
scider::plotROI(spe, roi = coi) + 
  ggtitle("Tumour cell-based ROIs")

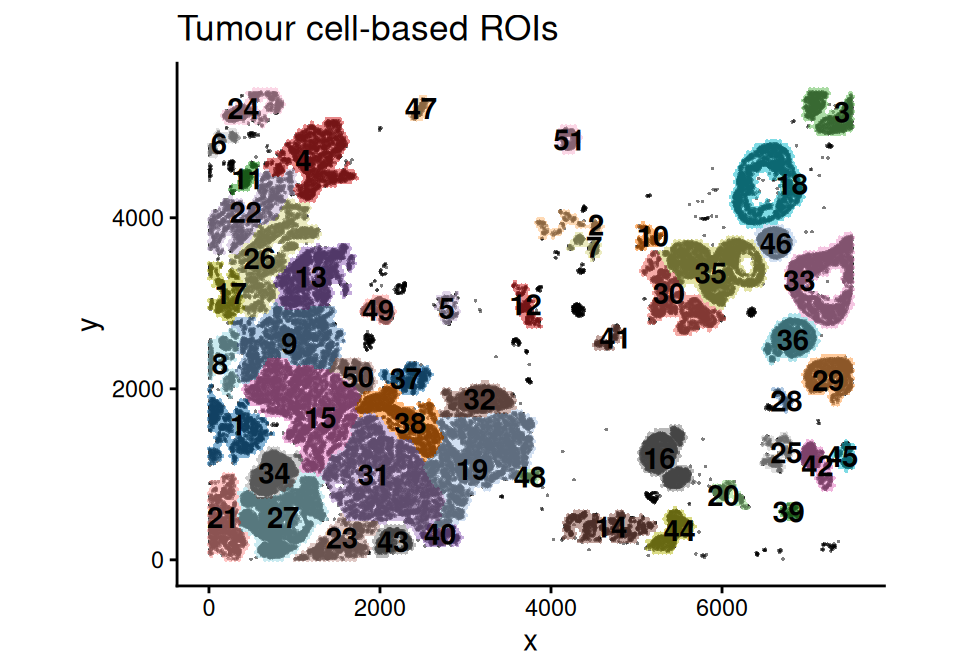
These ROIs can then be used for downstream analysis, such as cell type colocalization, spatial domain clustering, and differential expression (DE). Here as an example, we demonstrate an ROI-level cell type co-localization analysis.

20.5.1 Cell type co-localization on the ROI level

scider performs cell type co-localization analysis by calculating the correlation between the spatial densities of every two cell types.

Code

spe_cor <- corDensity(spe)
scider::plotCorHeatmap(spe_cor)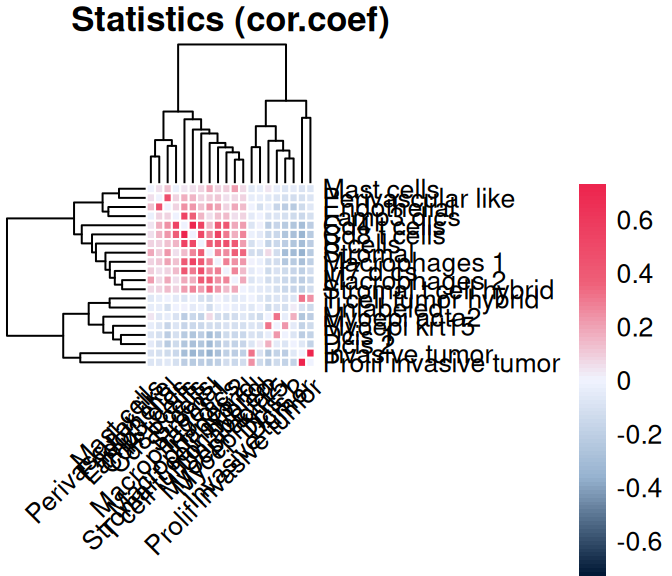

Cell type colocalization in tumor-specific ROIs.

We see that immune and stromal cells are positively colocalized within their respective groups, whereas myoepithelial, DCIS, and invasive tumor populations form distinct, negatively correlated clusters.

20.5.2 Cell type composition analysis based on density contours

Additionally, contour levels can be calculated from the estimated COI density, which is useful for cell type composition analysis.

Code

spe <- getContour(spe, coi = coi, bins = 10)
scider::plotContour(spe, coi = coi, line.width = 0.5)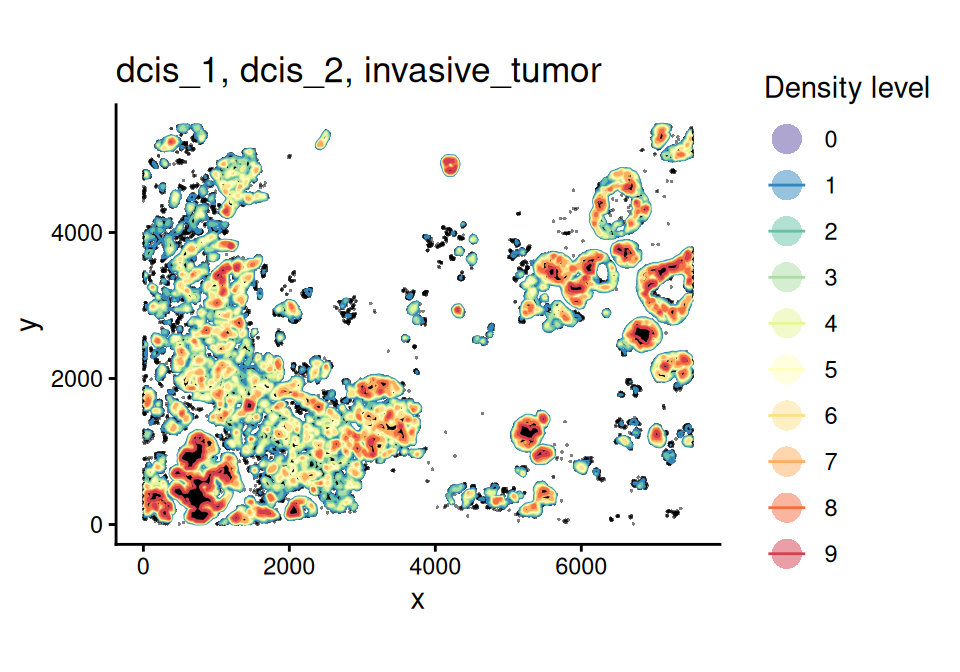

Spatial plot of contour lines calculated from the spatial density of tumor cells.

We can then assign each cell to its corresponding contour level according to their spatial coordinates, and visualize the cell type composition at each COI contour level using the plotCellCompo() function.

Code

spe <- allocateCells(spe, contour = coi, to.roi = TRUE)
scider::plotCellCompo(spe, contour = coi, self.included = FALSE)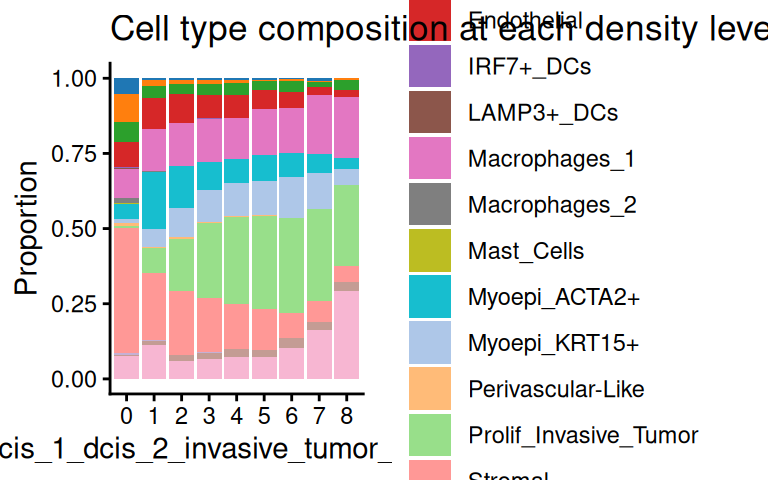

Cell type composition at each contour level of COI cells across all ROIs.

For example, we see a decreasing proportion of stromal cells, and an increasing proportion of unlabeled cells as tumor cell density increases. Normally, we would have filtered out unlabeled cells in preprocessing. It is also useful to investigate how cell type composition changes to COI densities within each ROI:

Code

scider::plotCellCompo(spe, contour = coi, self.included = FALSE, roi = coi)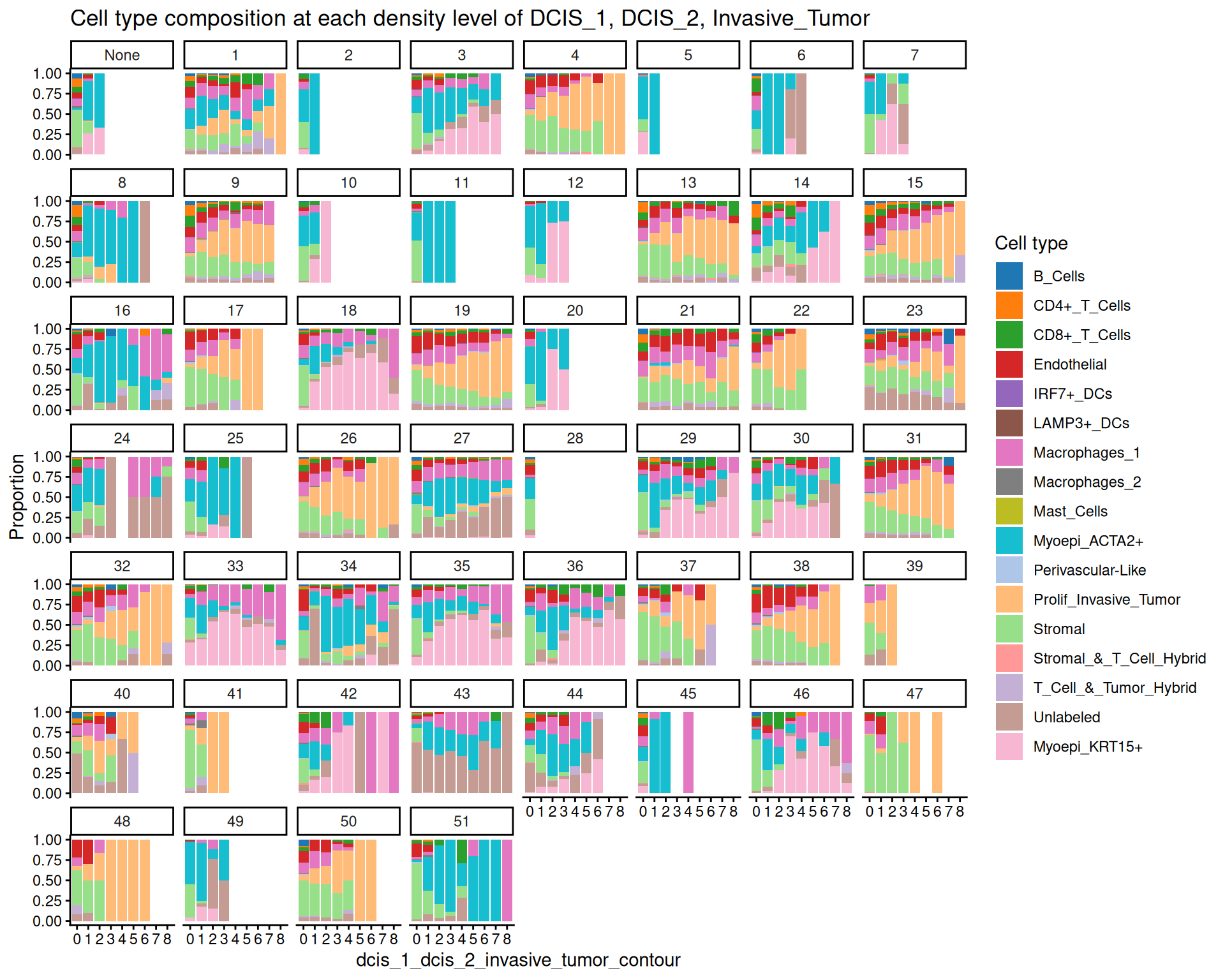

Cell type composition at each contour level of COI cells within each ROI.

ROIs can also be used to perform other types of downstream analysis, such as gene expression clustering, DE analysis and pathway analysis by pseudo-bulking cells located within each ROI, using the spe2PB() function. Given the pseudo-bulk samples, scider is fully compatible with all limma and edgeR functionalities, allowing arbitrarily complex experimental design to answer various biological questions. We recommend to perform such DE analyses using the voomLmFit() pipeline (Baldoni et al. 2025) or the quasi-likelihood pipeline in edgeR (Chen et al. 2025). Examples of DE and pathway analyses can be found in Li et al. (2025). More case studies will also be available at https://github.com/ChenLaboratory/scider.

20.6 Appendix

References

Baldoni, Pedro L., Lizhong Chen, Mengbo Li, Yunshun Chen, and Gordon K. Smyth. 2025. “Dividing Out Quantification Uncertainty Enables Assessment of Differential Transcript Usage with Limma and edgeR.” bioRxiv. https://doi.org/10.1101/2025.04.07.647659.

Chen, Yunshun, Lizhong Chen, Aaron T L Lun, Pedro L Baldoni, and Gordon K Smyth. 2025. “edgeR V4: Powerful Differential Analysis of Sequencing Data with Expanded Functionality and Improved Support for Small Counts and Larger Datasets.” Nucleic Acids Research 53 (gkaf018, 2). https://doi.org/10.1093/nar/gkaf018.

Janesick, Amanda, Robert Shelansky, Andrew D. Gottscho, Florian Wagner, Stephen R. Williams, Morgane Rouault, Ghezal Beliakoff, et al. 2023. “High Resolution Mapping of the Tumor Microenvironment Using Integrated Single-Cell, Spatial and in Situ Analysis.” Nature Communications 14 (8353). https://doi.org/10.1038/s41467-023-43458-x.

Li, Mengbo, Ning Liu, Quoc Hoang Nguyen, and Yunshun Chen. 2025. “Preserving Tissue Structure Through Density-Based Spatial Analysis with Scider.” bioRxiv. https://doi.org/10.1101/2025.09.11.675745.

Liu, Ning, Jarryd Martin, Dharmesh D Bhuva, Jinjin Chen, Mengbo Li, Samuel C. Lee, Malvika Kharbanda, et al. 2025. “hoodscanR: Profiling Single-Cell Neighborhoods in Spatial Transcriptomics Data.” bioRxiv. https://doi.org/10.1101/2024.03.26.586902.

Windhager, Jonas, Vito Riccardo Tomaso Zanotelli, Daniel Schulz, Lasse Meyer, Michelle Daniel, Bernd Bodenmiller, and Nils Eling. 2023. “An End-to-End Workflow for Multiplexed Image Processing and Analysis.” Nature Protocols 18: 3565–3613. https://doi.org/10.1038/s41596-023-00881-0.